최소 신장 트리
신장 트리란 순환 없이 모든 정점을 연결하는 그래프를, 최소 신장 트리란 모든 정점을 순환 없이 최소 간선 비용으로 모든정점을 연결하는 그래프를 말한다.

절단(Cut)

그래프를 절단(S, V-S) 하면 임의의 S라는 정점의 집합과, V-S 정점의 집합으로 분리된다.
교차(cross) / 존중(respect)
S의 정점와 V-S의 정점을 연결하는 간선을 교차(cross)한다고 부른다.

절단선을 기준으로 교차하지 않는 간선의 집합을 존중한다(respect)라고 한다.

경량 간선(light edge) / 안전 간선(safe edge)
절단선을 교차하는 간선 중 가중치가 최소인 간선을 경량 간선이라고 한다.
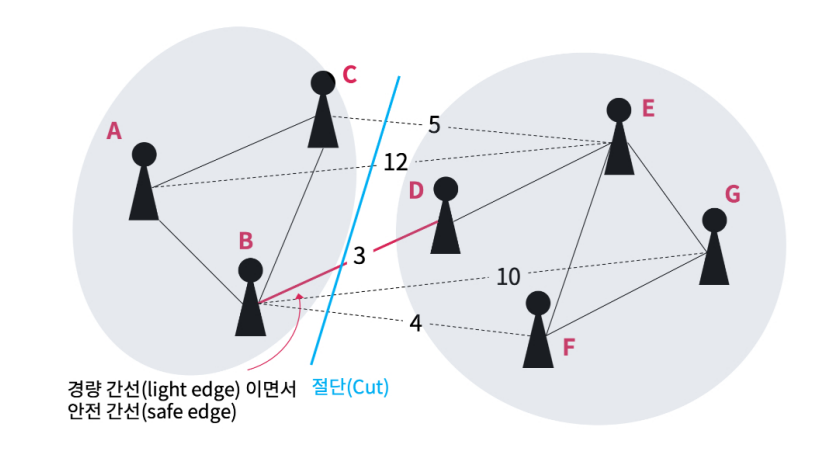
최소 신장 트리를 만족하며 루프 불변성을 유지하기 위해 경량 간선이면서 그래프를 순환하지 않도록 하는 간선을 안전 간선이라고 한다.
일반 알고리즘
최소 신장 트리의 일반 알고리즘은 여러 번 반복하더라도 A 집합이 최소 신장 트리를 만족하도록 하는 루프 불변성을 가지고 있다. 항상 A 집합에 안전 간선만 추가하기 때문에 루프의 중간에 A 집합을 확인하더라도 최소 신장 트리를 만족한다.
GENERIC_MST(G, w) {
A = 공집합
while A가 신장 트리를 형성하지 못한다
A에 대한 안전 간선(u,v)를 찾는다
A = A U {(u,v)}
return A;
}
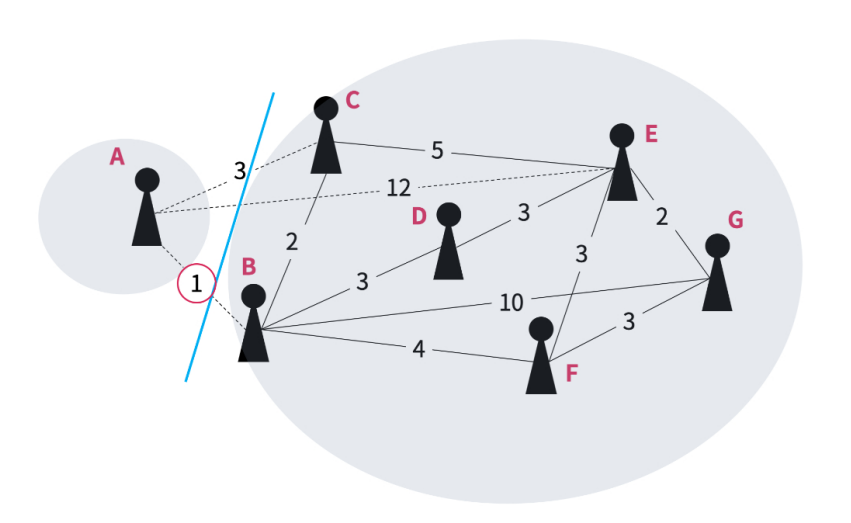
그래프를 임의로 절단한다고 가정
절단을 교차하는 간선 중 안전 간선은 가중치가 1인 간선 => 안전 간선을 A 간선 집합에 포함시킴
A 집합은 아직 신장 트리를 만족하지 못하므로 신장 트리를 만족할 때 까지 계속 반복적으로 절단하는 과정을 거침
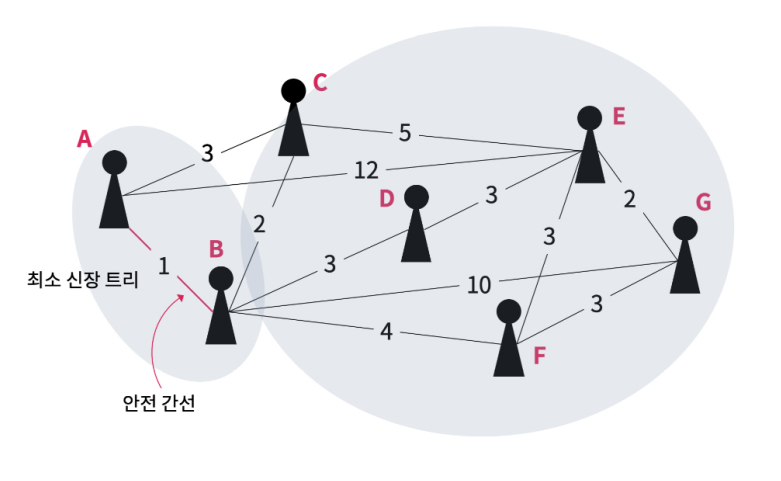
.
.
.
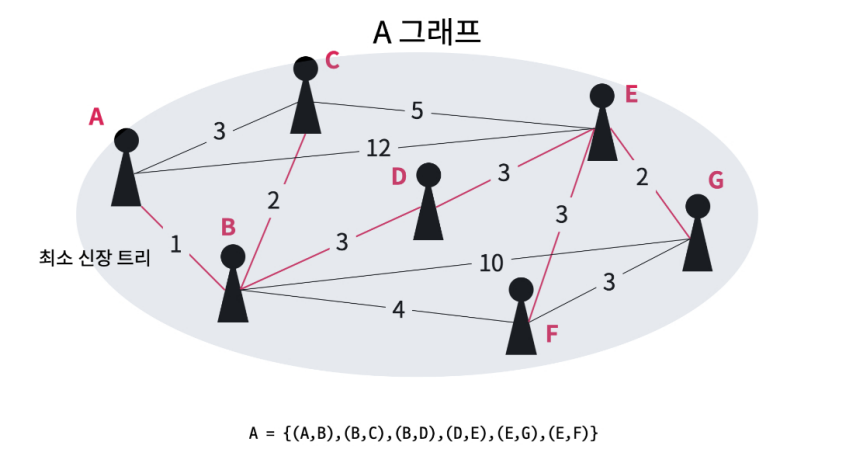
모든 간선이 연결되면 하나의 트리로 형성됨
크루스칼 알고리즘
크루스칼 알고리즘은 최소 신장 트리의 일반 알고리즘을 기반으로 하며 최소 가중치 순으로 간선을 확인하는 방식이다.
그래프의 간선의 집합을 가중치가 낮은 순으로 정렬하고, 간선의 가중치가 낮은 순으로 그래프를 절단한다. 그 다음 간선을 하나씨 확인하면서 안전 간선을 찾아 최소 신장 트리를 만족하는 간선의 집합을 형성한다.
예시로 아래와 같은 그래프가 있다. 간선은 가중치 순으로 정렬되어 있고, 각 정점의 대표 원소를 가리키는 서로소 집합 배열이 있다. 최초에는 서로소 부분 집합의 원소들이 자기 자신을 가리키고 있다.
서로소 집합
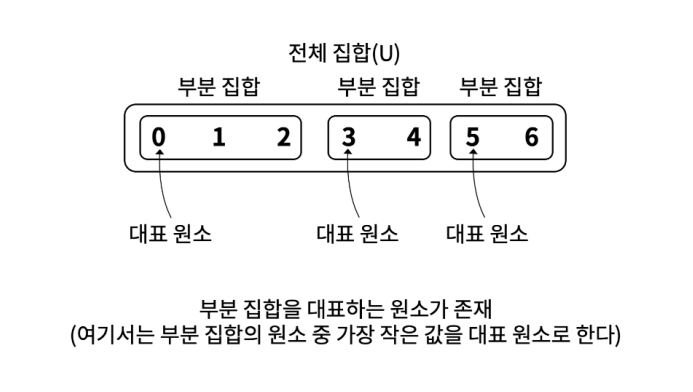
부분 집합끼리 서로 다른 원소를 가지고 있는 것을 서로소 집합이라 하며, 각 부분 집합에는 집합을 대표하는 대표 원소가 존재한다.
서로소 집합의 특징을 이용하여 간선의 순환 여부를 판단할 수 있다.
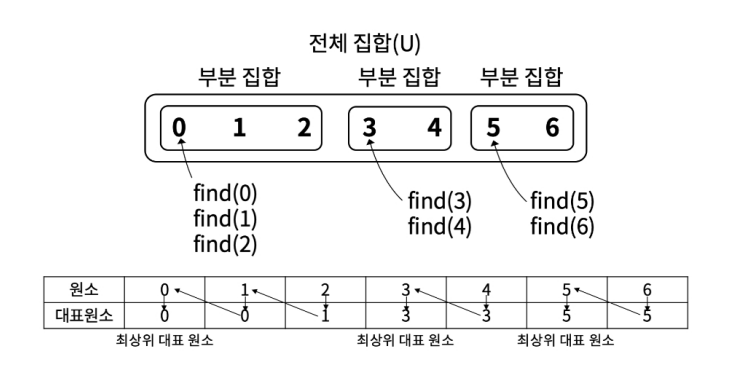
find() 연산
find 연산은 원소가 속한 부분 집합의 대표 원소를 반환하는연산으로,재귀적으로 실행되어 대표 원소를 탐색할 수 있다.
예시로 find(2)의 경우 2의 대표 원소는 1, 1의 대표 원소는 0, 0의 대표원소는 0이므로 0,1,2는 같은 부분 집합에 속해 있다고 할 수 있다.
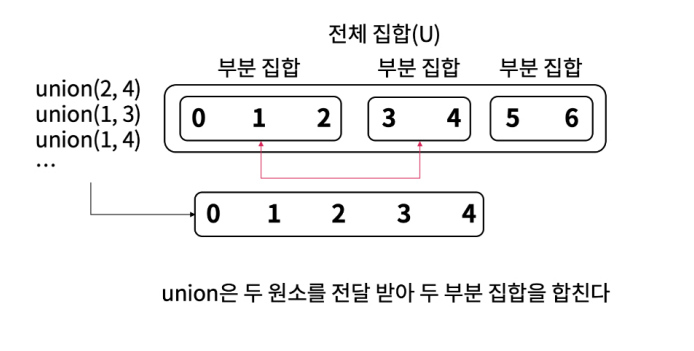
Union(... , ... ) 연산
union 연산은 두 서로소 집합을 하나의 집합으로 합친다. 두 개의 원소를 전달 받았을 때 서로 다른 부분 집합에 속해 있는 경우 최상위 대표 원소를 찾아 같은 대표 원소를 가리키도록 한다.
예시로 {0, 1, 2} 와 {3, 4} 부분 집합이 존재하고 union(1, 4) 하는 경우 원소 1의 최상위 대표 원소는 0이고, 원소 4의 최상위 대표 원소는 3이므로 3이 가리키고 있는 대표 원소를 0으로 변경해주면 된다.
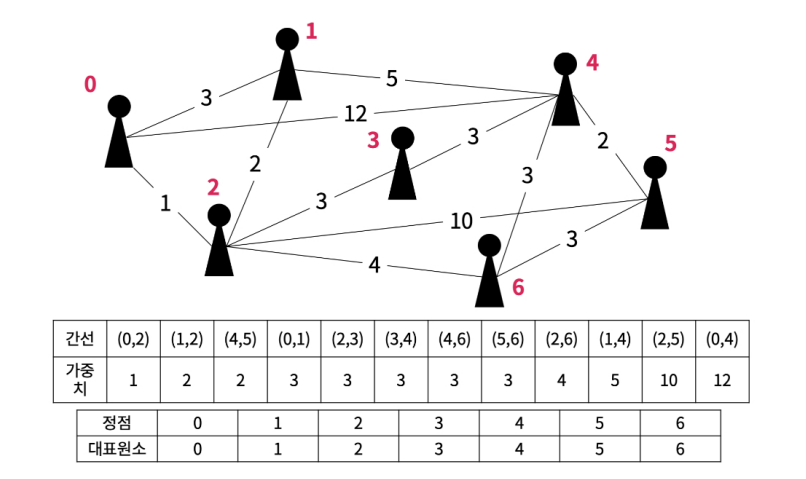
가장 먼저 (0, 2) 간선을 확인한다. 0번 정점과 2번 정점의 대표 원소를 확인하여 최상위 대표 원소가 서로 겹치지 않는다면 순환하지 않는 간선이므로 2번 정점의 대표 원소를 0으로 변경해 주고 안선 간선의 집합으로 추가한다.
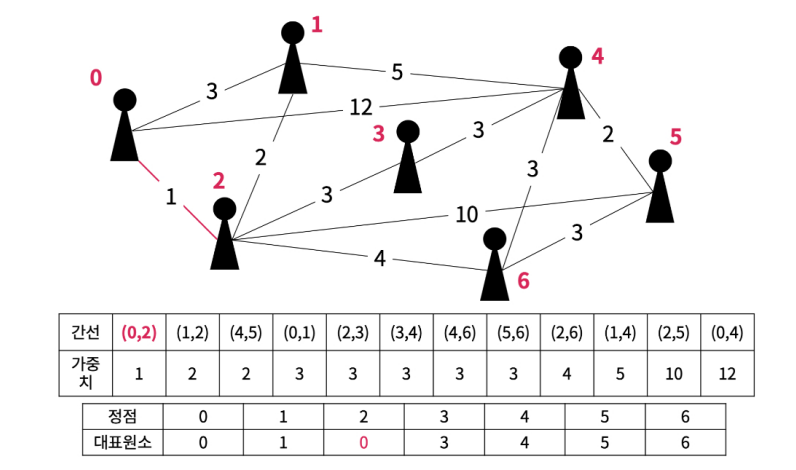
.
.
.
(0, 1) 간선을 확인했을 때 0번 정점과 1번 정점의 대표 원소는 모두 0으로 같은 부분 집합에 속해있다고 볼 수 있다. 따라서 해당 간선을 추가하면 순환이 발생하므로 그냥 넘어간다.
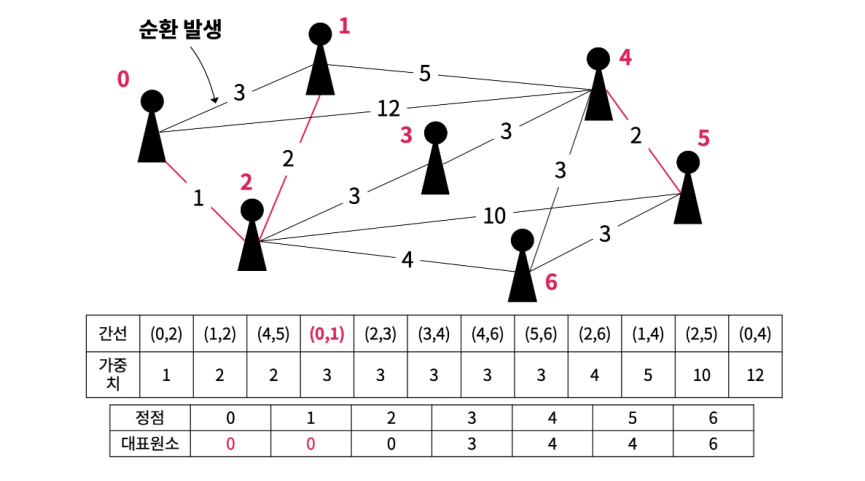
이런 식으로 모든 간선에 대한 확인이 끝나면 간선 집합에는 최소 신장 트리를 만족하는 안전 간선만 존재한다.
프림 알고리즘
프림 알고리즘은 너비 우선 탐색같이 정점을 방문 후 정점을 기준으로 부속된 간선들을 우선순위 큐에 가중치 순으로 저장하고, 큐에서 간선을 꺼내 방문하지 않은 정점들을 방문하며 안전 간선을 추가하는 알고리즘이다.
크루스칼 알고리즘이 안전 간선 집합이 포리스트(forest)를 형성한다면 프림 알고리즘은 하나의 최소 신장 트리를 유지하는 방식으로 진행된다.
PRIM_MST() {
vertex = 방문할 정점
priorityQueue;
while 방문하지 않은 정점이 존재한다
visit(vertex)
for 정점에 부속된 간선을 priorityQueue에 저장한다
if 간선의 정점을 방문하지 않았다
간선을 priorityQueue에 저장한다
while priorityQueue에 간선이 존재한다
edge = 큐에서 꺼낸 간선
if 간선의 정점을 방문하지 않았다
vertex = 간선의 도착지 정점
해당 간선을 안전 간선으로 추가한다
break;
}
예시로 아래와 같은 그래프가 있다고 가정한다. 방문 여부를 체크하는 배열과, 간선의 가중치 순대로 저장하는 우선순위 큐가 필요하다.
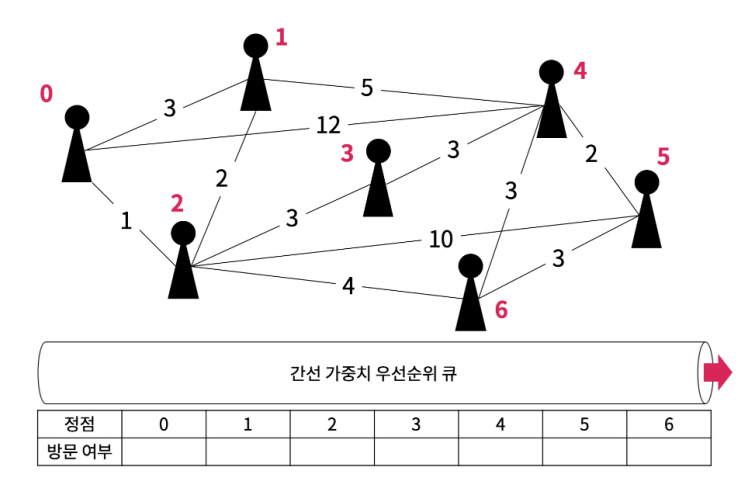
먼저 최초의 탐색 정점을 0으로 가정하고 방문 처리한다.
0번 정점 기준 부속된 간선들 중 도착지 기준 방문하지 않은 간선을 우선순위 큐에 저장한다. (가중치 순으로)
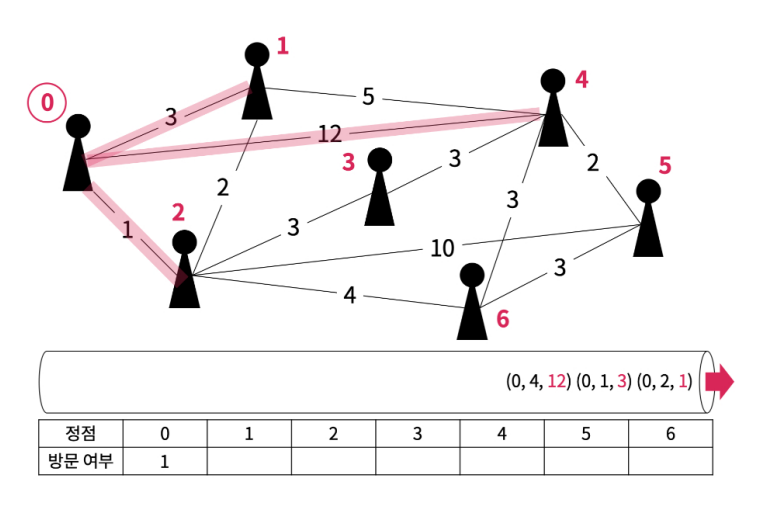
우선순위 큐에서 간선 하나를 꺼내서 도착지 기준 방문하지 않은 정점이면 해당 간선을 안전 간선으로 추가하고, 다음에 방문할 정점으로 2번 정점을 저장한다.
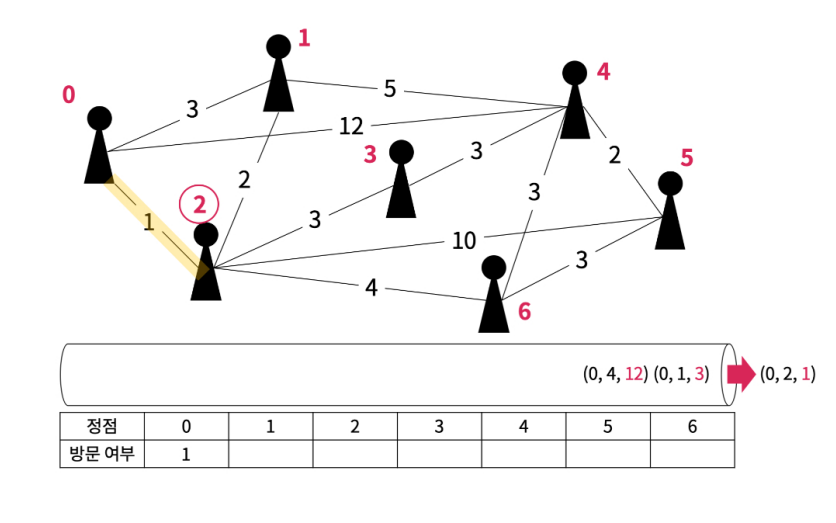
2번 정점을 방문 처리하고, 2번 정점 기준 부속된 간선들 중 도착지 기준 방문하지 않은 간선을 우선순위 큐에 저장한다.
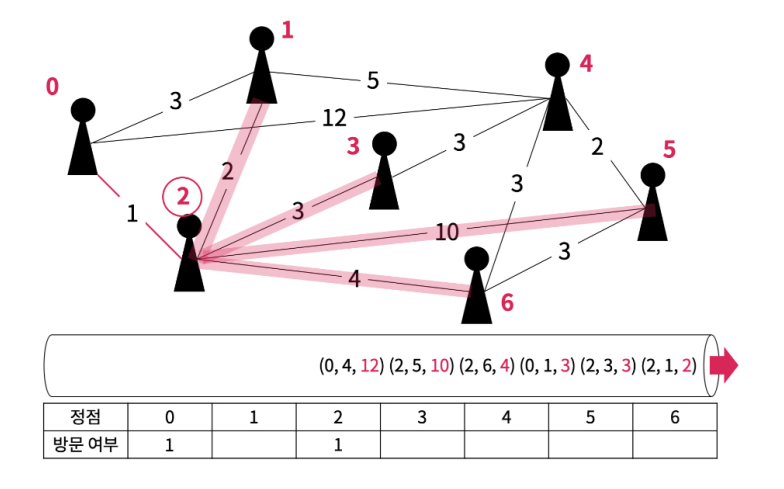
우선순위 큐에서 간선 하나를 꺼내서 도착지 기준 방문하지 않은 정점이면 해당 간선을 안전 간선으로 추가하고 다음에 방문할 정점으로 1번 정점을 저장한다.
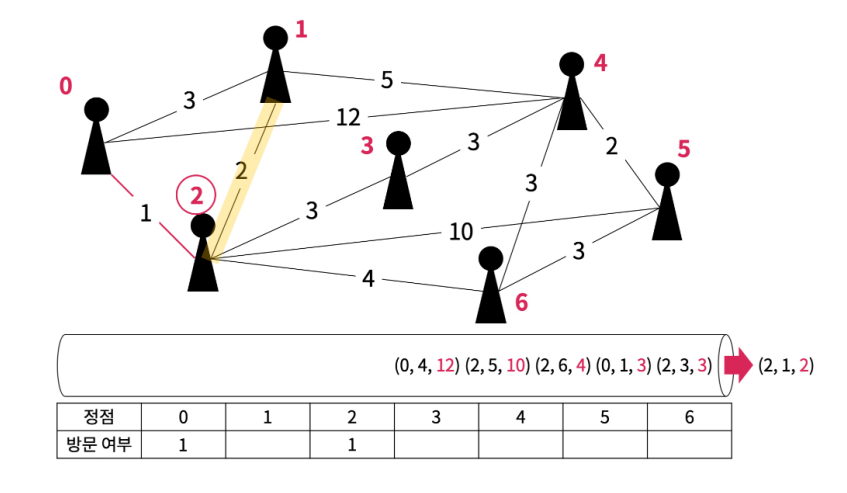
.
.
.
우선순위 큐에서 간선을 꺼냈을 때 도착지 기준 이미 방문했던 정점이면 해당 간선을 패스한다.
이렇게 프림 알고리즘은 정점 방문 시 부속된 간선들을 가중치 우선순위 큐에 저장하고 => 우선순위가 높은 순으로 간선을 하나씩 꺼내서 방문 여부를 판단한 뒤 방문하지 않았으면 안전 간선으로 추가하고 => 다음에 방문할 정점으로 정하는 방식으로 안전 간선의 루프 불변성을 유지하면서 최소 신장 트리를 만든다.
참조
https://www.codelatte.io/courses/java_data_structure
자바 자료구조 강의 - 코드라떼
컴퓨터 공학 2단계 자바 자료구조 강의입니다. 대부분의 프로그래밍하는 과정은 데이터를 다루는 일입니다. 데이터를 어떻게 잘 저장하고 관리할 수 있는지 자료구조에 대해 배웁니다. 자료구
www.codelatte.io
'6. 자료구조 & 알고리즘 > 6-1. 자료구조' 카테고리의 다른 글
| 자료구조 - [ 그래프 ] (0) | 2022.08.30 |
|---|---|
| 자료구조 - [ 해시 테이블 ] (0) | 2022.08.25 |
| 자료구조 - [ B-트리 ] (0) | 2022.08.24 |
| 자료구조 - [ Binary Heap ] (0) | 2022.08.23 |
| 자료구조 - [ Red-Black 트리 ] (0) | 2022.08.18 |
![자료구조 - [ 최소 신장 트리 ]](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FqeUOO%2FbtrK47sxTXU%2Fd4v04FQtIevZa8pjwyITFk%2Fimg.png)